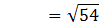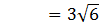Matematika Mudah: Agustus 2010

Rabu, 25 Agustus 2010

Jumlah dan Selisih Trigonometri

sin a + sin b = 2 sin 1/2(a + b) . cos 1/2(a - b)

sin a - sin b = 2 cos 1/2(a + b) . sin 1/2(a - b)

cos a + cos b = 2 cos 1/2(a + b) . cos 1/2(a - b)

cos a - cos b = -2 sin 1/2(a + b) . sin 1/2(a - b)

Pembuktian:

Rumus penjumlahan dan pengurangan merupakan bentuk lain dari rumus perkalian sinus dan kosinus

sin (α + β) + sin (α - β) = 2 sin α . cos β

sin (α + β) - sin (α - β) = 2 cos α. sin β

cos (α + β) + cos (α - β) = 2 cos α . cos β

cos (α + β) - cos (α - β) = -2 cos α . cos β

Misalkan α + β = a dan α - β = b maka:

α + β = a

α - β = b +

α = 1/2(a + b)

α + β = a

α - β = b -
β = 1/2(a - b)

Sehingga rumus jumlah da selisih sinus dan kosinus menjadi :

sin a + sin b = 2 sin 1/2(a + b) . cos 1/2(a - b)

sin a - sin b = 2 cos 1/2(a + b) . sin 1/2(a - b)

cos a + cos b = 2 cos 1/2(a + b) . cos 1/2(a - b)

cos a - cos b = -2 sin 1/2(a + b) . sin 1/2(a - b)

Contoh :
Tentukan nilai dari:

a. cos 75⁰ + cos 15⁰b. sin 75 ⁰ + sin 15⁰

Jawaban :

a. cos 75⁰ + cos 15⁰ = 2 cos ½(75⁰+15⁰) . cos ½(75⁰-15⁰)

= 2 cos 45⁰. cos 30⁰

= 2 . ½√2. ½√3

= ½√6

b. sin 75⁰ + sin 15⁰ = 2 sin ½(75⁰+15⁰) . cos ½(75⁰-15⁰)

= 2 sin 45⁰. cos 30⁰

= 2 . ½√2. ½√3

= ½√6

Jarak

Yang dimaksud dengan jarak antara dua buah bangun adalah panjang ruas garis penghubung terpendek yang menghubungkan dua titik pada bangun-bangun tersebut.

Jika G1 dan G2 adalah bangun bangun geometri, maka G1 dan G2 sebagai himpunan titik-titik, sehingga dapat dilakukan pemasangan antara titik-titik pada G1 dan G2.

Karena ruas garis AB adalah yang terpendek antara semua ruas garis penghubung titik-titik itu, maka panjang ruas garis AB disebut jarak antara bangun G1 dan G2

Jarak titik dan titik

Jarak antara dua buah titik A dan B adalah ruas garis AB
Jarak titik dan garis

Perhatikan titik penalti terhadap garis gawang.

Jarak titik P terhadap garis adalah ruas garis penghubung titik P dengan proyeksinya pada garis AB yaitu garis PP'

Jarak titik dan bidang

Jarak titik P terhadap bidang α adalah panjang ruas garis penghubung P dengan proyeksi titik P pada bidang α yaitu PP'

Contoh :

Diketahui kubus ABCD.EFGH dengan rusuk 6 cm. Hitunglah!

a. Jarak E ke C

b. Jarak E ke O

c. Jarak O ke DCGH

d. Jarak O ke FG

e. Jarak C ke AH

Jawab :

a. Jarak E ke C = EC = 6√3 cm

b. Jarak E ke O = EO

c. Jarak O ke DCGH = OP = 1/2 . AD = 3 cm

d. Jarak O ke FG

Bidang yang memuat titik O dan garis FG adalah ∆OFG.

Jarak O ke FG adalah OQ

e. Bidang yang memuat titik C dan garis AH adalah ∆ACH

Jarak C ke AH adalah CI

Jarak antara dua garis sejajar

Jarak antara dua garis sejajar adalah ruas garis yang tegak lurus dengan kedua garis tersebut

Garis PQ merupakan jarak antara k dan l

Jarak antara dua garis bersilang

Jarak dua garis bersilang k dan l adalah ruas garis penghubung terpendek antara dua buah titik di garis k dan l, dimana garis penghubung itu tegak lurus dengan garis k dan l.

Jarak antara garis k dan garis l adalah garis PQ

Jarak antara garis dan bidang sejajar

Jarak antara garis l dengan bidang α yang sejajar sama dengan jarak salah satu titik pada garis g terhadap bidang α

Jarak antara titik p dengan bidang α adalah garis PP'

Jarak antara dua bidang sejajar

Jarak antara bidang K dan bidang L yang sejajar sama dengan jarak salah satu titik pada bidang K terhadap bidang L, atau sebaliknya.

Jarak antara bidang ADHE dan bidang BCGF adalah ruas garis PP' = QQ'

Fungsi Kuadrat

Fungsi x pada himpunan R yang ditentukan oleh f(x) = ax² + bx + c, dengan a, b, c ∈R dan a ≠ 0, dinamakan fungsi kuadrat. Grafiknya berbentuk parabola.

Menggambar grafik fungsi kuadrat

Grafik fungsi kuadrat f(x) = ax² + bx + c adalah berupa parabola. Perlu diingat bahwa penulisan f(x) = ax² + bx + c dapat ditulis y = ax² + bx + c.

Untuk menggambar grafik y = ax² + bx + c, kita dapat melakukan langkah-langkah berikut:

Menentukan titik potong grafik di sumbu x (akar-akar persamaan kuadrat)
Menentukan persamaan sumbu simetri:
Menentukan titik puncak parabola

Puncak parabola merupakan pasangan berurutan dari sumbu simetri dengan nilai ekstrim (Nilai absolut / Nilai Mutlak)

Ciri-ciri parabola y = ax² + bx + c, dari tanda-tanda a, b, c, dan D

Apabila a > 0 maka parabola terbuka ke atas (mempunyai titik balik minimum)
Apabila a <>
Apabila tanda b sama dengan tanda a, maka puncak parabola berada di sebelah kiri sumbu y
Apabila b = 0, puncak parabola terletak pada sumbu y
Apabila a berlawanan dengan b , maka puncak parabola berada di sebelah kanan sumbu y
Apabila c > 0, maka parabola memotong sumbu y positif
Apabila c = 0, maka parabola melalui pusat koordinat
Apabila c <>
Apabila D > 0 maka parabola memotong sumbu x di dua titik
Apabila D = 0 maka parabola memotong sumbu x di satu titik
Apabila D > 0 maka parabola tidak memotong sumbu x

Sketsa grafik fungsi kuadrat:

Diskriminan

Persamaan kuadrat ax² + bx + c = 0 dapat diselesaikan dengan rumus abc :

Bentuk b² - 4ac pada rumus diatas disebut Diskriminan. Biasanya ditulis

D = b² - 4ac

Sehingga rumus abc dapat ditulis :

Nilai diskriminan menentukan jenis-jenis akar persamaan kuadrat yaitu :

Jika D > 0 maka persamaan kuadrat itu mempunyai dua akar real yang berbeda
Jika D = 0 maka persamaan kuadrat itu mempunyai dua akar real sama (akar kembar)
Jika D <>

Diskriminan persamaan kuadrat diantaranya digunakan untuk :

Menentukan nilai maksimum dan minimum
Mengetahui banyaknya titik potong parabola dengan sumbu x dan jenisnya
Menentukan koefisien-koefisien persamaan kuadrat yang akar-akarnya memenuhi sifat tertentu.

Deret Geometri Tak Hingga

Misalkan selembar kertas berbentuk segiempat dibagi menjadi 2 dan salah satu bagiannya dibagi lagi menjadi 2 bagian. Bagian ini dibagi lagi menjadi 2 dan begitu seterusnya seperti gambar berikut ini:

Secara teoritis pembagian ini dapat dilakukan berulang kali sampai tak hingga kali. Pada pembagian pertama diperoleh setengah bagian, yang kedua seperempat bagian, yang ketiga seperdelapan bagian dan seterusnya sampai tak hingga kali. Tampak jelas bahwa jumlah dari seluruh hasil pembagian sampai tak hingga kali tetap = kertas semula (1 bagian). Hasil ini dapat dituliskan:

Deret geometri tak hingga merupakan deret geometri yang banyak sukunya (n) tak hingga. Kita telah mengetahui bahwa untuk menentukan jumlah n suku pertama dari suatu deret geometri digunakan rumus:

Oleh karena yang dipelajari adalah deret geometri tak hingga maka akan ditinjau setiap nilai dari r untuk n → ∞ sebagai berikut:

Untuk r > 1 atau r < -1 Oleh karena r > 1 atau r < -1 maka nilai rⁿ akan semakin besar jika n makin besar. Dalam hal ini,
Untuk r > 1 dan n → ∞ maka rⁿ→ ∞
Untuk r < -1 dan n → ∞ maka rⁿ→ -∞.
Sehingga diperoleh

Deret geometri tak hingga dengan r > 1 atau r < -1 disebut deret divergen (menyebar) karena deret ini tidak memiliki kecendrungan pada suatu nilai tertentu. Oleh karena itu deret ini tidah memilik limit jumlah
Untuk -1 <>n akan semakin kecil dan mendekati nol. Dalam hal ini untuk n → ∞ maka rⁿ→ 0. Sehingga diperoleh

Deret geometri tak hingga dengan -1 <>

Contoh

Tentukan jumlah deret geometri tak hingga berikut.

Berdasarkan deret tersebut dapat kita ketahui a = 2 dan r = 1/3. Dengan demikian,

Jadi jumlah deret geometri tersebut adalah 3

Deret Geometri

Misalkan U₁, U₂, U₃, ..., U_n adalah barisan geometri maka penjumlahan

U₁ + U₂+ U₃ + ...+ U_n merupakan deret geometri.

Secara umum, dari suatu barisan geometri U₁, U₂, U₃, ..., U_n dengan U₁= a da rasio = r, kita dapat memperoleh bentuk umum penjumlahan deret geometri, yaitu
S_n = U₁ + U₂+ U₃ + ...+ U_n = a + ar + ar² + ... + ar^n-1

Untuk mendapatkan rumus n jumalah suku pertama dari deret geometri kita kalikan persamaan diatas dengan r, maka akan muncul persamaan baru:

(S_n . r) = ar + ar² + ar³ + ... + arⁿ

Selanjutnya kita eliminasi kedua persamaan tersebut dengan mengurangkannya:

S_n = a + ar + ar² + ... + ar^n-1

(S_n . r) = ar + ar² + ... + ar^n-1+ arⁿ -

S_n - (S_n . r) = a - arⁿ

S_n (1 - r) = a (1- rⁿ)

Jadi rumus n suku pertama deret geometri adalah:

a = suku pertama
r = rasio
n = banyaknya suku

Pada deret geometri juga berlaku sifat:

U_n= S_n - S_n-1

Deret Aritmatika

Deret aritmatika adalah penjumlahan barisan aritmatika. Misalkan U₁, U₂, U₃, ..., U_n adalah barisan aritmatika maka penjumlahan U₁ + U₂ + U₃ + ... + U_n adalah deret aritmatika.

Rumus jumlah n suku pertama pada deret aritmatika

S₁₀ = 20 + 30 + 40 + ... + 90 + 100 + 110

S₁₀ = 110 + 100 + 90 + ... + 40 + 30 + 20 ₊

2S₁₀= 130 + 130 + 130 + ... + 130 + 130 + 130

2S₁₀= 10 x 130

2S₁₀= 10 x ( 20 + 110 )

S₁₀ = 1/2 x 10 x ( 20 + 110 )

Kita dapat melihat angka 10 didapat dari banyaknya suku (n), 130 didapat dari penjumlahan suku awal (a) dan suku akhir (U_n). Maka diperoleh:

S_n= 1/2 n (a + U_n)

Karena U_n= a + (n-1)b, maka

S_n= 1/2 n (2a + (n-1) b)

Dari pengertian n suku pertama barisan aritmatika didapat sifat berikut :

S_n = U₁ + U₂ + U₃ + ... + U_n-1 + U_n

S_n-1 = U₁ + U₂ + U₃ + ... + U_n-1 +

S_n - S_n-1 = U_n

U_n = S_n - S_n-1

Jika U_n adalah suku ke n barisan aritmatika dan S_n adalah jumlah n suku pertama barisan aritmatika maka berlaku sifat

U_n = S_n - S_n-1

Contoh 1

Diketahui deret aritmatika : 5 + 11 + 17 + 23 + ...
a. Tentukan rumus jumlah n suku pertamanya
b. Hitung jumlah 30 suku pertama

a. S_n= 1/2 n (2a + (n-1) b)

= 1/2 n (2(5) + (n-1)6)

= 5n + (n-1)3n

= 5n + 3n² - 3n

Jadi S_n = 3n² + 2n

b. S₃₀ = 3(30)² + 2(30) = 2760

Contoh 2:

Hitunglah 3 + 8 + 13 + ... + 98

Jawab:

a = 3, b = 5, Un = 98

Un = a + (n - 1)b

98 = 3 + (n - 1)5

98 = 3 + 5n - 5

5n = 100

n = 20

Jumlah deret itu adalah S₂₀ = 1/2. 20 (3 + 98) = 1110

Bilangan Cacah

Pengertian

Bilangan cacah adalah himpunan bilangan bulat yang tidak negatif, yaitu {0, 1, 2, 3 ...}. Dengan kata lain himpunan bilangan asli ditambah 0. Jadi, bilangan cacah harus bertanda positif. Himpunan bilangan cacah :

C = {0, 1, 2, 3, 4, ....}

Himpunan bilangan cacah memuat beberapa bilangan antara lain :

Himpunan bilangan asli A = { 1, 2, 3, 4, ...}
Himpunan bilangan genap = {0, 2, 4, 6, ...}
Himpunan bilangan ganjil = {1, 3, 5, 7, ...}
Himpunan bilangan kuadrat = {0, 1, 4, 9, ...}
Himpunan bilangan prima = {2, 3, 5, 7, ...}
Himpunan bilangan tersusun (komposit) = {4, 6, 8, 12, ...}

Operasi pada bilangan cacah

Penjumlahan
- komutatif : a + b = b + a
- asosiatif : (a + b) + c = a + (b + c)
- unsur identitas (netral) adalah nol (0)
- sifat tertutup pada penjumlahan
  Penjumlahan dua atau lebih bilangan cacah selalu menghasilkan bilangan cacah
Pengurangan adalah operasi kebalikan dari penjumlahan a - b = c, sama artinya dengan b + c = a.
Perkalian
- komutatif : a x b = b x a
- asosiatif : (a x b) x c = a x (b x c)
- distributif :
  a x (b + c) = (a x b) + (a x c)
  a x (b - c) = (a x b) - (a x c)
- unsur identitas perkalian adalah satu (1)
  a x 1 = a
  b x 1 = b
- semua bilangan cacah dikalikan dengan nol (0), hasilnya nol (0)
  a x 0 = 0
  b x 0 = 0
- sifat tertutup perkalian
  semua perkalian bilangan cacah menghasilkan bilangan cacah juga.
Pembagian
- Pembagian adalah operasi kebalikan dari perkalian
  a : b = c ⟹ b x c = a
- 0 dibagi dengan bilangan cacah (kecuali 0), hasilnya nol (0)
- pembagian dengan 0 tidak didefinisikan.

Barisan Geometri

Misalkan U₁, U₂, U₃, ..., U_n suatu barisan bilangan. Barisan bilangan tersebut dikatakan barisan geometri apabila memenuhi

r adalah rasio atau pembanding. Dibawah ini adalah beberapa contoh dari barisan geometri.

2, 4, 8, 16, 32, 64, ... maka rasio = 4/2 = 8/4 = 16/8 dan seterusnya
27, 9, 3, 1, 1/3, ... maka rasio = 27/9 = 9/3 = 3/1 dan seterusnya

Rumus suku ke- n barisan geometri

Jika diketahui suatu barisan bilangan geometri U₁, U₂, U₃, ..., U_n, dan U₁= a dengan rasionya r maka kita dapat menuliskan:

U₁= a

U₂= U₁.r = a.r = ar^2-1

U₃= U₂.r = (ar).r = ar^3-1

U₄= U₃.r = (ar²).r = ar^4-1

U_n= ar^n-1

Jadi rumus umum suku ke- n barisan geometri adalah

U_n= ar^n-1

Suku tengah barisan geometri

Perhatikan barisan geometri berikut

a, ar, ar², ar³, ar⁴, ar⁵, ar⁶

Bila diambil 3 suku saja yaitu a, ar, ar². Maka Ut = ar, U₁ = a, U_n= ar²U₁.U_n= a²r², maka Ut = akar a²r²

Bila diambil 5 suku maka Ut = ar², U₁ = a, U_n= ar⁴U₁.U_n= a²r⁴, maka Ut = akar a²r⁴. Bagitu juga seterusnya.

Sehingga bila diambil n suku maka

dan suku tengah tersebut terletak pada urutan ke 1/2 (n + 1)

Sisipan barisan geometri

Misalkan U₁, U₂ adalah dua suku berurutan dari suatu barisa geometri dengan rasio r. Diantara U₁ dan U₂ disisipkan k buah bilangan sehingga terbentuk barisan geometri baru dengan rasio r', maka barisan baru yang terbentuk adalah

U₁, U₁.r', U₁.r'², ..., U₁.r'^k, U₂

Perbandingan antara dua suku yang berurutan tetap = r' maka