Secara teoritis pembagian ini dapat dilakukan berulang kali sampai tak hingga kali. Pada pembagian pertama diperoleh setengah bagian, yang kedua seperempat bagian, yang ketiga seperdelapan bagian dan seterusnya sampai tak hingga kali. Tampak jelas bahwa jumlah dari seluruh hasil pembagian sampai tak hingga kali tetap = kertas semula (1 bagian). Hasil ini dapat dituliskan:
Deret geometri tak hingga merupakan deret geometri yang banyak sukunya (n) tak hingga. Kita telah mengetahui bahwa untuk menentukan jumlah n suku pertama dari suatu deret geometri digunakan rumus:
Oleh karena yang dipelajari adalah deret geometri tak hingga maka akan ditinjau setiap nilai dari r untuk n → ∞ sebagai berikut:
- Untuk r > 1 atau r < -1 Oleh karena r > 1 atau r < -1 maka nilai rn akan semakin besar jika n makin besar. Dalam hal ini,
Untuk r > 1 dan n → ∞ maka rn→ ∞
Untuk r < -1 dan n → ∞ maka rn→ -∞.
Sehingga diperoleh
Deret geometri tak hingga dengan r > 1 atau r < -1 disebut deret divergen (menyebar) karena deret ini tidak memiliki kecendrungan pada suatu nilai tertentu. Oleh karena itu deret ini tidah memilik limit jumlah - Untuk -1 <>n akan semakin kecil dan mendekati nol. Dalam hal ini untuk n → ∞ maka rn→ 0. Sehingga diperoleh

Deret geometri tak hingga dengan -1 <>
Contoh
Tentukan jumlah deret geometri tak hingga berikut.
Berdasarkan deret tersebut dapat kita ketahui a = 2 dan r = 1/3. Dengan demikian,
Jadi jumlah deret geometri tersebut adalah 3


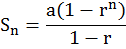



0 komentar:
Posting Komentar