Jarak

Yang dimaksud dengan jarak antara dua buah bangun adalah panjang ruas garis penghubung terpendek yang menghubungkan dua titik pada bangun-bangun tersebut.

Jika G1 dan G2 adalah bangun bangun geometri, maka G1 dan G2 sebagai himpunan titik-titik, sehingga dapat dilakukan pemasangan antara titik-titik pada G1 dan G2.

Karena ruas garis AB adalah yang terpendek antara semua ruas garis penghubung titik-titik itu, maka panjang ruas garis AB disebut jarak antara bangun G1 dan G2

1. Jarak titik dan titik
   
   
   
   Jarak antara dua buah titik A dan B adalah ruas garis AB
   
   
2. Jarak titik dan garis
   
   Perhatikan titik penalti terhadap garis gawang.
   
   
   
   Jarak titik P terhadap garis adalah ruas garis penghubung titik P dengan proyeksinya pada garis AB yaitu garis PP'
   


3. Jarak titik dan bidang
   
   
   
   Jarak titik P terhadap bidang α adalah panjang ruas garis penghubung P dengan proyeksi titik P pada bidang α yaitu PP'
   
   Contoh :
   
   Diketahui kubus ABCD.EFGH dengan rusuk 6 cm. Hitunglah!
   
   
   
   a. Jarak E ke C
   
   b. Jarak E ke O
   
   c. Jarak O ke DCGH
   
   d. Jarak O ke FG
   
   e. Jarak C ke AH
   
   
   
   Jawab :
   
   
   
   a. Jarak E ke C = EC = 6√3 cm
   
   b. Jarak E ke O = EO
   
   
   
   
   
   
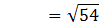
   c. Jarak O ke DCGH = OP = 1/2 . AD = 3 cm
   
   d. Jarak O ke FG
   
   Bidang yang memuat titik O dan garis FG adalah ∆OFG.
   
   
   
   Jarak O ke FG adalah OQ
   
   
   
   
   
   
   
   e. Bidang yang memuat titik C dan garis AH adalah ∆ACH
   
   
   
   
   Jarak C ke AH adalah CI
   
   
   
   
   
   
   
   


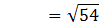
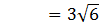
4. Jarak antara dua garis sejajar
   
   Jarak antara dua garis sejajar adalah ruas garis yang tegak lurus dengan kedua garis tersebut
   
   
   
   Garis PQ merupakan jarak antara k dan l
   


5. Jarak antara dua garis bersilang
   
   Jarak dua garis bersilang k dan l adalah ruas garis penghubung terpendek antara dua buah titik di garis k dan l, dimana garis penghubung itu tegak lurus dengan garis k dan l.
   
   
   
   Jarak antara garis k dan garis l adalah garis PQ
   


6. Jarak antara garis dan bidang sejajar
   
   Jarak antara garis l dengan bidang α yang sejajar sama dengan jarak salah satu titik pada garis g terhadap bidang α
   
   
   
   Jarak antara titik p dengan bidang α adalah garis PP'
   
   
   
   


7. Jarak antara dua bidang sejajar
   
   Jarak antara bidang K dan bidang L yang sejajar sama dengan jarak salah satu titik pada bidang K terhadap bidang L, atau sebaliknya.
   
   
   
   Jarak antara bidang ADHE dan bidang BCGF adalah ruas garis PP' = QQ'